Entropie dvou obálek

O paradoxu dvou obálek jsem již psal. Pro připomenutí, nacházíte se v situaci, kterou jsem ve zmíněném příspěvku popsal jako televizní soutěž, kde:

Moderátor před vás položí dvě obálky, a sdělí vám, že uvnitř jsou šeky na výherní částku. Také vám sdělí, že z těchto dvou částek je ta vyšší dvojnásobkem té nižší. Nesdělí vám ale už, o jak vysoké částky se jedná.

Podle pravidel si teď musíte vybrat právě jednu z obálek. Poté ji máte právo otevřít a podívat se, o jakou částku se jedná. Nebude-li se vám částka líbit, můžete obálku vrátit a vzít tu druhou, ovšem tato volba je již definitivní.

Zdánlivý paradox spočívá v tom, že na jednu stranu je celkem očividně jedno, jestli vezmu první nebo druhou obálku. Před otevřením jsou obě obálky rovnocenné, a otevřením jedné z obálek se nic nedozvím o tom, jestli je to ta s více penězi nebo ta s méně penězi. Na druhé straně ovšem, najdu-li v obálce částku X, očekávaná střední hodnota v druhé obálce je 5X/4, což by znamenalo, že je lepší brát druhou obálku.

Napsal jsem, že paradoxnost vymizí, pokud blíže určíme, co znamená, že částky v obálkách jsou náhodné. Když řekneme, že nějaké číslo je náhodné, intuitivně automaticky předpokládáme, že její rozdělení je rovnoměrné na oboru přípustných hodnot, tj. že každá přípustná hodnota má stejnou pravděpodobnost. Ovšem na intervalu (0, ∞) rovnoměrné rozdělení neexistuje. U jakéhokoli jiného rozdělení ale neplatí, že otevřením jedné z obálek se nic nedozvím. Což jsem ilustroval na dvou příkladech.

Mohl jsem se tvářit, že problém je vyřešen, ale svět bohužel (nebo naštěstí) není tak jednoduchý. Není totiž od věci trvat na původním zadání: máte dvě obálky, o nichž vám moderátor sdělí právě jenom to, že v jedné je X, v druhé 2X, a X je náhodné. Vašim úkolem je zvolit strategii postupu.

Namítat, že pojem náhodnosti není jednoznačný, nepomůže. Ne vždy člověk dostává přesné a jednoznačné informace. Náhodnost X nemusí být výsledkem stisknutí tlačítka RND na kalkulačce či sledováním rozpadu uranu 235 či čehokoli jiného, co vnímáme jako z podstaty náhodný děj. Klidně to může být tak, že X si moderátor vycucal z prstu, nebo je pevně určeno v pravidlech soutěže, která vy bohužel neznáte. Pravděpodobnost nakonec není nějaká mysteriózní síla, která řídí určitou uzavřenou třídu jevů. Pravděpodobnost nežije v obálkách ani v náhodných generátorech; naopak, žije v našich hlavách, kde popisuje míru naší (ne)znalosti faktů. A v tomto případě je to tak, že o hodnotě X nevíme vůbec nic, a jsme nuceni si vymyslet její rozdělení pravděpodobnosti.

Pokud bychom věděli, že X může nabývat jen omezeného intervalu hodnot, automaticky volíme rozdělení rovnoměrné. Zdá se to naprosto přirozené, ačkoli není vůbec jednoduché odpovědět na otázku, proč. Není žádný pevný logický princip, který by nás k tomu nutil. Můžeme mávat rukama a říkat, že nemáme žádný důvod předpokládat, že pravděpodobnost, že při hodu mincí padne líc je větší nebo menší než pravděpodobnost, že padne rub - a proto předpokládáme, že tyto pravděpodobnosti jsou stejné. Na druhé straně, není-li důvod předpokládat různost těchto pravděpodobností, není ani důvod předpokládat jejich stejnost [1]. Pokud je nějaký fakt těžko odůvodnitelný, obvykle se to řeší tak, že jej prohlásíme za princip či axiom. S takovým "řešením" se tady můžeme klidně spokojit, a prohlásit, že při absenci jakýchkoli informací o hodnotě X kromě znalosti intervalu přípustných hodnot, z principu přiřazujeme X rovnoměrnou pravděpodobnost na onom intervalu.

Existuje nějaký podobný princip, který funguje i na nekonečných intervalech? Ukazuje se, že ano: za určitých podmínek poslouží princip maximální entropie [2].

Entropie pravděpodobnostního rozdělení je definována jako

S = -Σi pi log pi ,

přičemž pro spojité rozdělení je suma nahrazena integrálem. Číslo pi je pravděpodobnost i-té hodnoty. Základ logaritmu může být jakýkoli, nehraje to žádnou zásadní roli. (Omezuji se zde pouze na praktický popis principu, nikoli na argumenty, kterými je podpořen. Speciálně by stálo za to rozebrat, proč je entropie definována zrovna tak, jak je definována; snad se k tomu někdy v budoucnu dostanu.)

Princip maximální entropie říká (dále jen PME), že člověk by měl neznámé veličině přiřadit takové rozdělení, které má ze všech přípustných rozdělení nejvyšší entropii. Ukazuje se, že pro omezené intervaly dává PME rovnoměrné rozdělení, takže PME je zobecněním jednoduššího "principu rovnoměrné pravděpodobnosti", či jak tomu chceme říkat. Pro ilustraci vezměme hod mincí. Pravděpodobnost, že padne líc, označmě p, pravděpodobnost pádu rubu je bezpochyby 1-p. PME říká, že

- p ln p - (1-p) ln(1-p)

má být maximální, což je pro p = 1/2. [3]

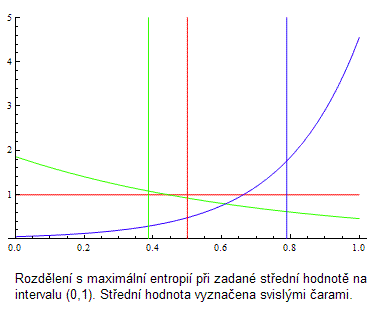
Síla PME samozřejmě nespočívá ve schopnosti dojít k rovnoměrnému rozdělení neznámé veličiny v případě, že nevíme nic než obor jejích přípustných hodnot. To bychom mohli postulovat rovnou. Pomocí PME ale jsme schopni najít "správné" rozdělení i v případě, kdy máme o veličině dodatečné informace. Typickým případem je, když máme důvod se domnívat, že známe její střední hodnotu. Potom nám PME dá exponenciální rozdělení [4], jak můžeme vidět na třech příkladech na obrázku níže:

Uvažujeme-li interval (0, ∞), rozdělení s maximální entropií bez dodatečné podmínky na něm neexistuje. Čímž by se mohlo zdát, že nám PME nijak nepomohl. Ale ve skutečnosti jsme na tom docela dobře. Stačí totiž, specifikujeme-li střední hodnotu neznámé veličiny, a PME nám nadiktuje

rozdělení (bude to, stejně jako u konečného intervalu, exponenciála). (Kdybychom hledali rozdělení na intervalu (-∞, ∞), museli bychom zadat ještě jednu podmínku - mohl by to být třeba rozptyl a v takovém případě by rozdělení s nejvyšší entropií byla Gaussova křivka.)

Díky PME se tedy naše situace zjednodušuje. Místo celého rozdělení nám stačí nějak odhadnout jeho střední hodnotu. Na otázku jak bohužel žádná standardní odpověď neexistuje. Můžeme například odhadnout, kolik zhruba peněz si pořadatel soutěže může dovolit věnovat na výhru. Je celkem těžké si představit situaci, kdy není k dispozici žádná vědomost, která by mohla být použita k odhadu střední hodnoty. A i kdyby nebyla, střední hodnotu prostě odhadneme náhodně, ať už to znamená cokoli - nebude to pořád o nic horší, než kdybychom neměli žádnou strategii.

Princip maximální entropie se tak nejeví jako moc velká výhra. Což se není čemu divit, pokud máme málo informací, naše rozhodování podle toho bude vypadat, i když bude podrobeno matematickému formalismu. Pokud ale jsme schopni aspoň nějakou informaci získat, pak PME nabývá na síle. Představme si, že jsme dvojobálkové loterii podrobeni opakovaně. Pak můžeme evidovat výsledky z předchozích opakování a z nich spočítat odhady střední hodnoty, rozptylu a dalších momentů, ty pak zadat jako dodatečné podmínky pro hledané rozdělení a najít to s největší entropií. Tato strategie by měla být velmi efektivní.

Není samozřejmě pravda, že takový postup bude vždy optimální strategií. Házím-li cinknutou kostkou, na které padne vždycky šestka, také není optimální předpokládat rovnoměrné rozdělení. Optimální je předpokládat, že padne vždy šestka. Pokud ovšem vím, že je kostka cinknutá, ale nevím jak konkrétně, zase mi nezbyde než předpokládat rovnoměrné rozdělení. Předpoklad, že padne vždy šestka je sice optimální na kostce, která je tak upravena, ale je naprosto nevhodný na drtivé většině ostatních kostek. Naopak zásada rovnoměrného rozdělení padajících hodnot je univerzální. Stejně tak univerzální, ale obecnější, je princip maximální entropie. Obecnější proto, že umožňuje vzít v úvahu částečně známé informace. A dává odpověď na otázku: Jaké je přirozené rozdělení náhodné veličiny na nekonečném intervalu?

Poznámky:
1. Hod mincí není moc dobrý příklad, protože s ním máme dlouhodobé zkušenosti. Asi každý si za život pár set krát hodil mincí a ví proto, že rub a líc padají přibližně stejně často. Pokud ale narazíme na jev, se kterým žádnou zkušenost nemáme, je nastalá situace prekérnější.
2. Souvislost s termodynamikou je zde velmi volná. Ačkoli se člověk běžně s pojmem entropie setkává v souvislostech fyzikálních, pojem entropie přirozeně patří do teorie pravděpodobnosti a jeho fyzikální interpretace je jen jeho velmi specifickým uplatněním. Fyzikové ovšem objevili entropii nejdříve, již v
devatenáctém století. Princip maximální entropie pro pravděpodobnostní rozdělení byl formulován až v polovině století dvacátého.
3. Derivováním podle p získáme ln p - 1 + ln(1-p) + 1 = ln(1-p)/p, což je rovno nule právě když p = 1 - p.
4. Odvození je triviální úloha na variační počet.